人們撰寫了大量文章來闡述如何端接PCB走線特性阻抗以避免信號反射。但是，妥善運用傳輸線路技術的時機尚未說清楚。

下面總結了針對邏輯信號的一條成熟的適用性指導方針。

當PCB走線單向傳播延時等于或大于施加信號上升/下降時間(以最快邊沿為準)時端接傳輸線路特性阻抗。

例如，在E_r = 4.0介電質上2英寸微帶線的延時約270 ps。嚴格貫徹上述規(guī)則，只要信號上升時間不到~500 ps，端接是適當的。

更保守的規(guī)則是使用2英寸(PCB走線長度)/納秒(上升/下降時間)規(guī)則。如果信號走線超過此走線長度/速度準則，則應使用端接。

例如，如果高速邏輯上升/下降時間為5 ns，PCB走線等于或大于10英寸(其中測量長度包括曲折線)，就應端接其特性阻抗。

在模擬域內，必須注意，運算放大器和其他電路也應同樣適用這條2英寸/納秒指導方針，以確定是否需要傳輸線路技術。例如，如果放大器必須輸出最大頻率f_max，則等效上升時間t_r和這個f_max相關。這個限制上升時間t_r可計算如下：

t_r=0.35/f_max    等式1

然后將t_r乘以2英寸/納秒來計算最大PCB走線長度。例如，最大頻率100 MHz對應于3.5 ns的上升時間，所以載送此信號的7英寸或以上走線應視為傳輸線路。

PCB板上受控阻抗走線的設計

在受控阻抗設計中，可以采用多種走線幾何形狀，既可與PCB布局圖合二為一，也可與其相結合。在下面的討論中，基本模式遵循IPC標準2141A的規(guī)定(見參考文獻1)。

請注意，下面的圖示中將使用術語“接地層”。需要了解的是，該接地層實際上是一個大面積、低阻抗的參考層。在實踐中，可能是一個接地層或電源層，假定二者的交流電位均為零。

首先是簡單的平面上布線形式的傳輸線路，也稱微帶線。圖1所示為橫截面視圖。這類傳輸線路可能是實驗板中使用的信號線。其構成非常簡單，一條分立的絕緣線以固定間距分布于接地層上。介電質既可能是線材的絕緣層，也可能是該絕緣層與空氣的結合體。

圖1：一種阻抗既定的微帶線傳輸線路由一條分布于接地層的絕緣線形成

該線路的阻抗(單位：歐姆)可以用等式2估算。其中，D為導體直徑，H為線材在接地層上的間距，­ε_r為介電常數。

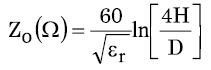等式2

對于與PCB相融合的圖形，有多種幾何模型可供選擇，分為單端和差分兩類。這些在IPC標準2141A(見參考文獻1)中有詳細說明，這里對兩個常見示例略加說明。

在開始進行任何基于PCB傳輸線路設計時，必須知道，有大量的等式都聲稱適用于此類設計。此時，一個極其重要的問題就是，“哪些等式是精確的呢？”不幸的是，沒有一個等式是完全精確的！所有現有等式都是近似值，因而，其精度不盡相同，取決于具體情況。最知名也是引用最多的是參考文獻1中給出的等式，但是，即使這些等式也存在一些應用問題。

參考文獻2針對不同幾何圖形，在試驗PCB樣品上對參考文獻1中的等式進行了評估。結果發(fā)現，預測精度因目標阻抗而異。下面引述的等式均來自參考文獻1，這里只是作為設計的起點，實際設計時，還需要進一步的分析、測試和進行設計驗證。原則就是，要仔細研究，謹慎面對PCB走線阻抗等式。

微帶線PCB傳輸線路

對于其中一面為接地層的簡單雙面PCB設計，可以在另一面設計一條信號走線以控制阻抗。這種幾何圖形被稱為表面微帶，簡稱微帶。

圖2中的雙層PCB橫截面視圖展示了這種微帶幾何圖形。

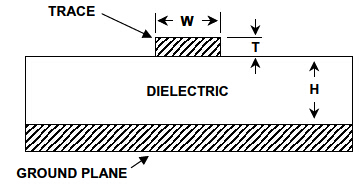
圖2：一種阻抗既定微帶傳輸線路由一條分布于接地層、采用適當幾何圖形的PCB走線形成

對于給定的PCB基板和銅重量，需要注意的是，W(信號走線寬度)以外的所有參數都是事先確定的。因而，可用等式3來設計一種PCB走線，以匹配電路要求的阻抗。若信號走線寬W、厚T，且由介電常數為­­ε_r的PCB電介質以距離H與接地層(或電源層)相分離，則其特性阻抗為：

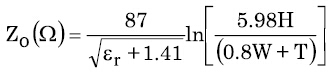等式3

請注意，在這些表達式中，測量值均為常用單位(mil)。

這些傳輸線路不但有特性阻抗，也有特性電容。其計算單位為pF/in，如等式4所示。

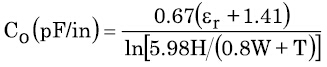等式4

作為包括這些計算的示例，一塊雙層板可能用20 mil寬(W)、1盎司(T=1.4)的銅走線，并由10 mil (H) FR-4 (­­ε_r= 4.0)的介電材料分離。結果，該微帶線的阻抗為50 Ω左右。對于其他標準阻抗(如75Ω的視頻標準阻抗)，使"W"調整為8.3 mil左右即可。

微帶線設計的一些指導原則

本例涉及到一個有趣且微妙的要點。參考文獻2討論了與微帶PCB阻抗相關的有用指導原則。若介電常數為4.0 (FR-4)，結果顯示，當W/H為2/1時，阻抗將接近50Ω­(與第一個示例類似，其中，W = 20 mil)。

仔細的讀者會發(fā)現，根據等式3預測，Z_o應為46Ω­左右，與參考文獻2提到的精度(>5%)相吻合。IPC微帶線等式在50Ω­與100 ­Ω之間最精確，但當阻抗低于或超過該范圍時，其精度則大幅下降。

根據等式5，也可以計算微帶線的傳播延遲。這是微帶信號走線的單向通過時間。有趣的是，對于給定的幾何模型，延遲常數(單位：ns/ft)僅為介電常數而非走線維度的函數(見參考文獻6)。請注意，這可以帶來極大的便利。意味著，當給定PCB基板(并給定­ε_r)時，各種阻抗線路的傳播延遲常數是固定不變的。

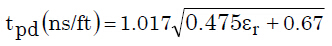等式5

該延遲常數也可以ps/in為單位，這樣更適用于小型PCB。即：

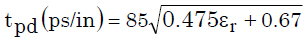等式6

因此，舉例來說，對于PCB介電常數4.0，不難發(fā)現微帶線的延遲常數約為1.63 ns/ft，合136 ps/in。這兩條額外的準則對于設計PCB走線中信號的時序具有參考意義。

對稱帶狀線PCB傳輸線路

從多種角度來看，多層PCB是一種更好的PCB設計方法。在這種模式下，信號走線嵌入電源層與接地層之間，如圖3中的橫截面視圖所示。低阻抗交流接地層和嵌入的信號走線形成一條對稱帶狀線傳輸線路。

從圖中可以看出，高頻信號走線的電流回路直接位于接地層/電源層上的信號走線的上方和下方。因此，高頻信號被完全限制在PCB板內部，結果使放射降至最低，為輸入雜散信號提供了天然的屏障。

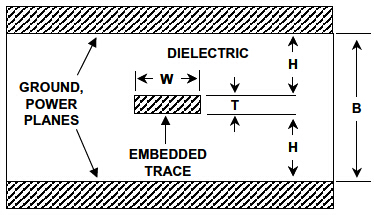
Figure 3: A Symmetric Stripline Transmission Line With Defined Impedance is Formed by a PCB Trace of Appropriate Geometry Embedded Between Equally Spaced Ground and/or Power Planes

該設計的特性阻抗同樣取決于幾何圖形以及PCB介電質的­­ε_r。該帶狀傳輸線路的Z_O可表示為：

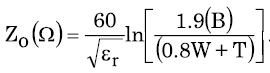等式7

這里的所有維度同樣以mil為單位，B為兩個層的間距。在這種對稱幾何圖形中，需要注意的是，B同樣等于2H + T。參考文獻2指出，參考文獻1中的這個等式的精度通常在6%左右。

適用于­ε_r= 4.0的對稱帶狀線的另一條便利準則是，使B成為W的倍數，范圍為2至2.2。結果將得到約50Ω的帶狀線阻抗。當然，這條法則是以另一近似法為基礎的，忽略了T。盡管如此，該法則對于粗略估算還是很有用的。

對稱帶狀線同樣有一個特性電容，其計算單位為pF/in，如等式8所示。

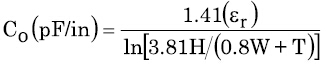等式8

對稱帶狀線的傳播延遲如等式9所示。

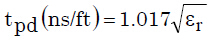等式9

或者以ps為單位：

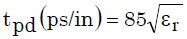等式10

當PCB介電常數為4.0時，可以發(fā)現，對稱帶狀線的延遲常數幾乎正好為2 ns/ft­，合170 ps/in。

走線嵌入法的利弊

根據上述討論，在設計阻抗既定的PCB走線時，既可以置于一個表層之上，也可嵌入兩層之間。當然，在這些阻抗因素之外，還有許多其他考慮因素。

嵌入式信號確實存在一個明顯的大問題——隱藏電路走線的調試非常困難，甚至無法做到。圖4總結了嵌入式信號走線的利弊。

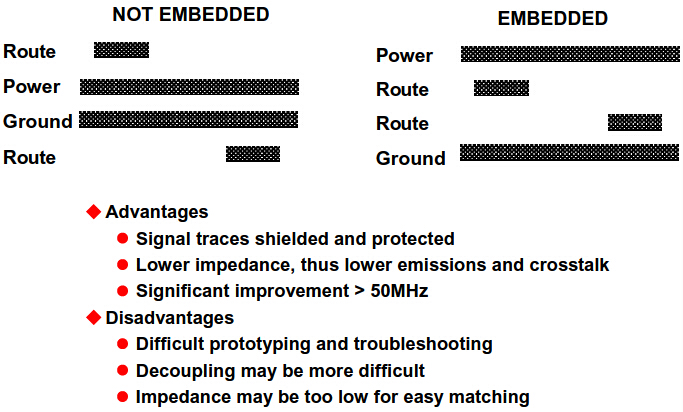
圖4：多層PCB設計中嵌入與不嵌入信號走線的利弊

設計多層PCB時也可能不使用嵌入式走線，如最左邊的橫截面視圖所示。可以將這種嵌入式設計看作一種雙重雙層PCB設計(共有四層銅)。頂部的走線與電源層構成微帶，底部的走線則與接地層構成微帶。在本例中，兩個外層的信號走線可以方便地供測量和故障排查使用。但這種設計并未利用各層的屏蔽作用。

這種非嵌入式設計的輻射量較大，更容易受到外部信號的影響，而右側的嵌入式設計采用了嵌入法，則很好地利用了各層的優(yōu)勢。就如諸多其他工程設計一樣，PCB設計中到底采用嵌入法還是非嵌入法是折衷的結果。這里的折衷則體現在減少輻射與方便測試之間。

參考文獻：

1. Standard IPC-2141A, "Controlled Impedance Circuit Boards and High Speed Logic Design," 2004, Institute for Interconnection and Packaging Electronic Circuits, 3000 Lakeside Drive, 309 S, Bannockburn, IL 60015, 847-615-7100.
2. Eric Bogatin, BTS015, PCB Impedance Design: Beyond the IPC Recommendations, BeTheSignal.com.
3. Eric Bogatin, Signal Integrity – Simplified, Prentice Hall PTR, 2003, ISBN-10: 0130669466, ISBN-13: 978-0130669469.
4. Andrew Burkhardt, Christopher Gregg, Alan Staniforth, "Calculation of PCB Track Impedance," Technical Paper S-19-5, presented at the IPC Printed Circuits Expo '99 Conference, March 14–18, 1999.
5. Brian C. Wadell, Transmission Line Design Handbook, Artech House, Norwood, MA, 1991, ISBN: 0- 89006-436-9.
6. William R. Blood, Jr., MECL System Design Handbook (HB205/D, Rev. 1A May 1988), ON Semiconductor, August, 2000.
7. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 12
8. Walt Kester, Analog-Digital Conversion, Analog Devices, 2004, ISBN 0-916550-27-3, Chapter 9. Also available as The Data Conversion Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7841-0, Chapter 9.
9. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Chapter 7. Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 7.

來源：Analog Devices, Inc.