1.前言
本系列自開篇以來陸續推出了基于python的線陣天線自動化設計,展現了python在陣列天線設計領域巨大的潛力,是人工智能與天線設計的一次親密接觸。我們為廣大讀者展現了使用python設計不同線陣的應用,通過自動化設計,大大提升了天線的設計效率,提高了工作效率。

圖1陣列天線自動設計
2.均勻線陣
常見的線陣綜合法主要有均勻幅度法、切比雪夫綜合法和泰勒綜合法,其中,切比雪夫和泰勒綜合法是實現低副瓣陣列天線的兩種方法,具有副瓣電平可控的特性。作為本系列線陣的結束篇,回顧一下切比雪夫綜合法和泰勒綜合法。
2.1 切比雪夫綜合法
P階切比雪夫多項式如下:
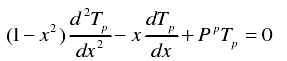
當p為偶數時 ,Tp見下式:
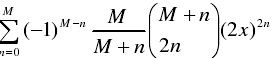
當p為奇數時 ,Tp見下式:
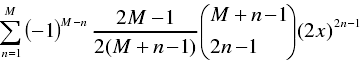
其中的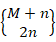 =
=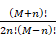
當天線的波瓣特性和切比雪夫多項式曲線一致時,該天線輻射特性具有切比雪夫特性,此時旁瓣的幅度都均相等。
由上式可知,當陣列單元為偶數階時,其陣因子如下:
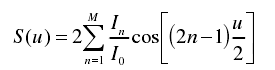
當陣列單元為奇數階時,其陣因子如下:
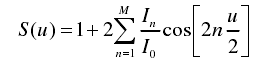
式中,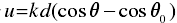 。
。
依據單元數為奇偶分以下情況得到對應的電流幅度。
a) 對于單元數為奇數的陣列
對于單元數為奇數的陣列而言,中心單元的激勵幅度為:
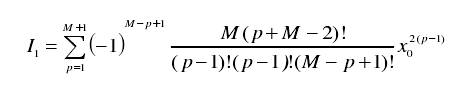
其一側的相對單元激勵幅度為:
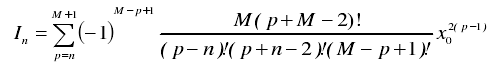
b) 對于單元數為偶數的陣列
其一側的相對單元激勵幅度為:
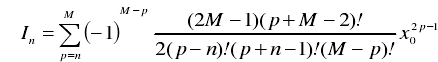
2.2 泰勒綜合法
泰勒綜合法的線陣輻射特性具有如下特點:
- 主瓣兩側的若干副瓣電平大小相似;
- 其余區域副瓣電平會單調減小。
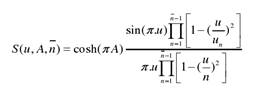
由以上特點可知,陣列天線的激勵從中間往兩側會單調遞減,不會發生切比雪夫綜合法中的跳變現象,方向圖函數為:
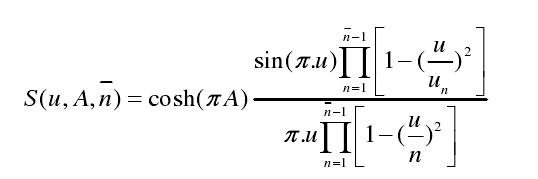
上式為構造的泰勒空間因子,具有理想空間因子可調副瓣電平和前n-1個副瓣電平接近相等的性質,同時在遠區副瓣保持了基本函數的副瓣峰值,也具備μ-1的衰減特性。其零點位置為:
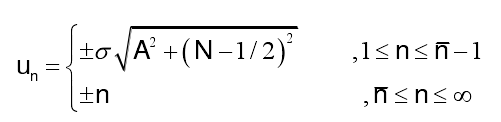
式中,
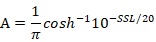
1)若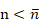 時,副瓣可稱為近旁瓣,近似相等;反之副瓣稱為遠旁瓣,逐漸衰減,。上式的u取整數時,即為方向圖零點位置。
時,副瓣可稱為近旁瓣,近似相等;反之副瓣稱為遠旁瓣,逐漸衰減,。上式的u取整數時,即為方向圖零點位置。
2)若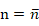 時,零點重合,有下式:
時,零點重合,有下式:
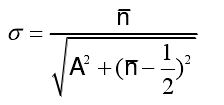
當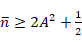 時,得到的陣列方向圖函數即為:
時,得到的陣列方向圖函數即為:
令天線陣列饋電幅度分布為I(ξ),其具有的泰勒分布如下圖所示。
a) 泰勒連續分布
泰勒連續分布示意圖如圖 1所示。
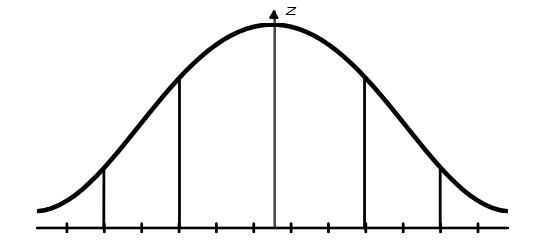
圖 2 泰勒分布示意圖
對應的連續電流分布為:
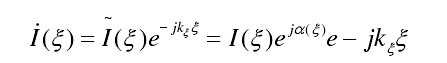
其中,kξ表示均勻相位常數,α(ξ)是非均勻相位常數,由上圖可知,電流分布具有對稱性,則該分布對應的陣列單元輻射陣因子為:
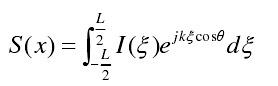
- X=i=0時,泰勒方向圖函數 S(x)=1;
- X=i小于n時,S(x)為:
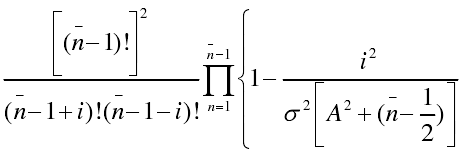
- X=i大于n時,S(x)=0。
口徑場分布函數I(ξ)為:
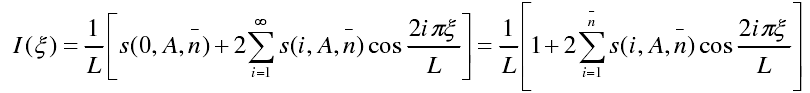
b)離散化
對于線陣而言,需要對上圖進行離散化,每個抽樣值對應著直線陣列上的單元激勵,利用抽樣定理,可以增加抽樣點使陣列單元的對應的幅度分布來貼合泰勒分布的連續線源幅度。
離散化后,每個陣元的坐標位置為:
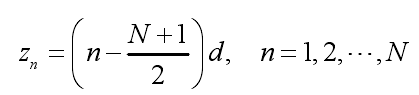
各單元對應的激勵電流幅度為:
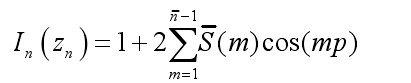
式中,p=2Πzn/L,L=Nd
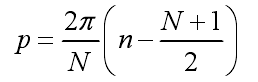
這里的,S(m)為:
- m=0時,泰勒方向圖函數 S(m)=1;
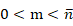 時,S(m)為:
時,S(m)為:
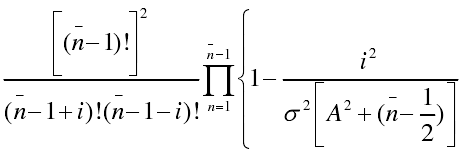
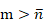 時,S(m)=0。
時,S(m)=0。
該式說明,對泰勒線源進行抽樣時,抽樣結果只與抽樣點數相關,可以看出激勵幅度與單元數量有關,而和單元間距無關。
下面展示了基于泰勒綜合法的20元陣列和40元陣列得到的方向圖,可看到陣元數越多,天線主瓣波束越窄。
- 單元數為20,陣元間距d為λ,指向0度
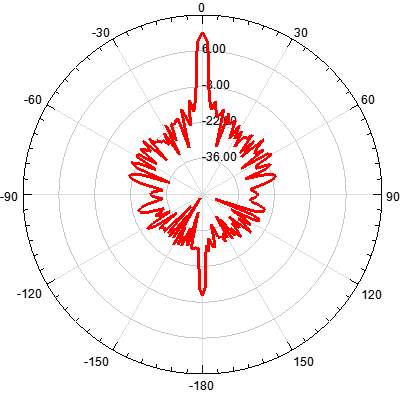
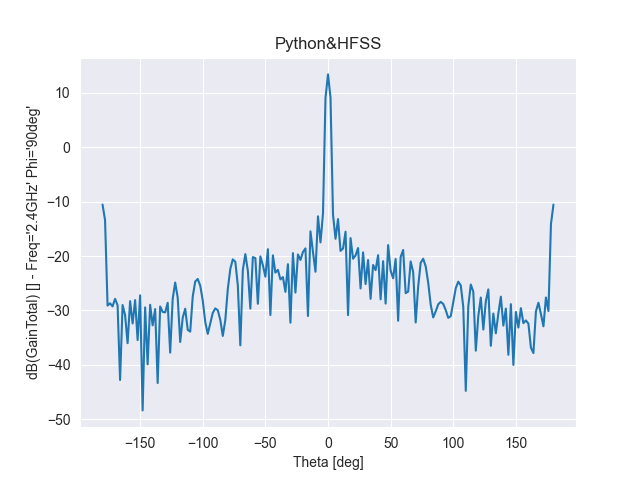
圖 3 20陣元天線
- 單元數為40,陣元間距為d為λ,指向0度
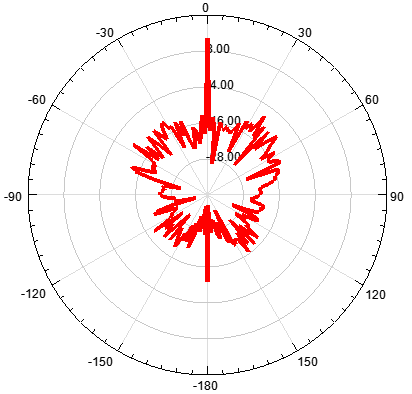
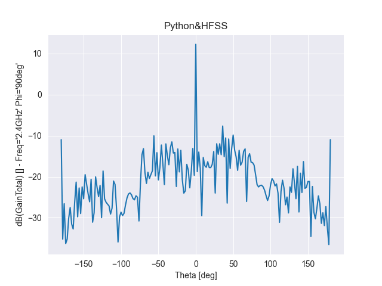
圖 4 40陣元天線
- 無人機陣列干擾天線設計
根據當前項目需求,設計一款2.4GHz的無人機平面陣列干擾天線,陣元如下圖所示,該天線陣元可展寬天線工作帶寬,同時有利于饋電設計。
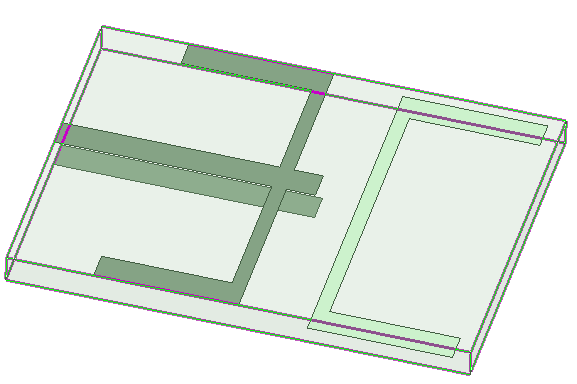
圖 5 陣元結構圖
結合上一節分析性的結果,這里該陣列干擾天線采用泰勒綜合法抑制副瓣電平,實現了12dBi的天線增益,該平面天線不增加重量及體積,同時高增益有助于增強對無人機遠程干擾能力,下圖分別給出陣列天線的方向圖與增益。
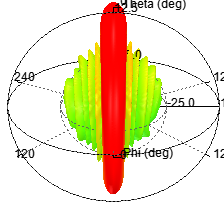
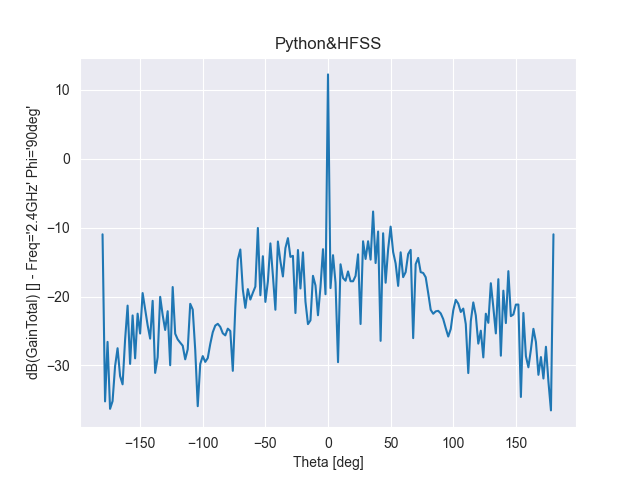
圖 6 干擾天線方向圖
工程實施時,該天線安裝在云臺上,通過陀機控制云臺方位與俯仰,對目標無人機實施干擾。
作者:江右射頻

 粵公網安備 44030902003195號
粵公網安備 44030902003195號