1 前言

前篇介紹了切比雪夫綜合法得到低副瓣特性的陣列天線，由上篇分析可知，等幅激勵(lì)的均勻線陣的副瓣電平幅度較高，可使用切比雪夫綜合法、泰勒綜合法實(shí)現(xiàn)陣列天線的方向圖低副瓣特性。當(dāng)天線的陣元個(gè)數(shù)超越一定范圍時(shí)，切比雪夫的兩端的電流差距很大，陣列天線兩端的單元會(huì)發(fā)生突然的跳變的現(xiàn)象，影響天線的低副瓣效果。因此，切比雪夫綜合法在某些雷達(dá)系統(tǒng)中并不是很適用，為了解決這一問(wèn)題，下面將介紹泰勒綜合法。

圖 1陣列天線自動(dòng)設(shè)計(jì)

2 基于泰勒綜合法的均勻陣列

泰勒綜合法是實(shí)現(xiàn)低副瓣陣列天線的一種方法，具有副瓣電平可控的特性，并且由于副瓣的遞減特性不會(huì)出現(xiàn)切比雪夫綜合法里面兩端突然跳變的現(xiàn)象，降低饋電網(wǎng)絡(luò)設(shè)計(jì)的復(fù)雜度，并且還會(huì)增強(qiáng)天線的方向性在工程上得到了廣泛的認(rèn)可。輻射特性具有如下特點(diǎn)：

1. 主瓣兩側(cè)的若干副瓣電平大小相似；
2. 其余區(qū)域副瓣電平會(huì)單調(diào)減小。

由以上特點(diǎn)可知，陣列天線的激勵(lì)從中間往兩側(cè)會(huì)單調(diào)遞減，不會(huì)發(fā)生切比雪夫綜合法中的跳變現(xiàn)象，方向圖函數(shù)為：

上式為構(gòu)造的泰勒空間因子，具有理想空間因子可調(diào)副瓣電平和前n-1個(gè)副瓣電平接近相等的性質(zhì)，同時(shí)在遠(yuǎn)區(qū)副瓣保持了基本函數(shù)的副瓣峰值，也具備μ^-1的衰減特性。其零點(diǎn)位置為：

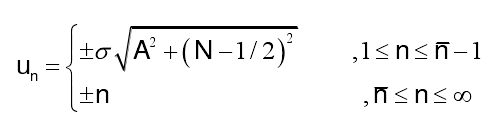
式中，

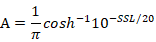
1）若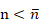時(shí)，副瓣可稱為近旁瓣，近似相等；反之副瓣稱為遠(yuǎn)旁瓣，逐漸衰減，。上式的u取整數(shù)時(shí)，即為方向圖零點(diǎn)位置。

2）若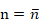時(shí)，零點(diǎn)重合，有下式：

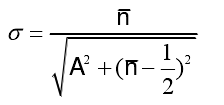
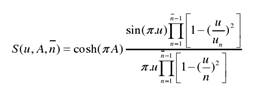
當(dāng)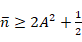時(shí)，得到的陣列方向圖函數(shù)即為：

令天線陣列饋電幅度分布為I(ξ)，其具有的泰勒分布如下圖所示。

a) 泰勒連續(xù)分布

泰勒連續(xù)分布示意圖如圖 1所示。

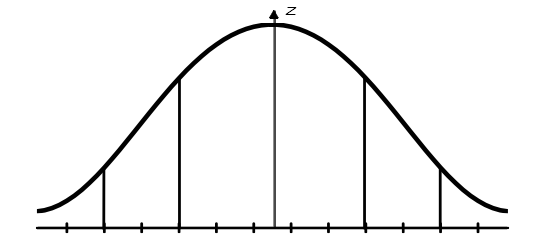
圖 2 泰勒分布示意圖

對(duì)應(yīng)的連續(xù)電流分布為：

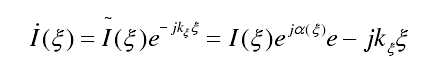
其中，k_ξ表示均勻相位常數(shù)，α(ξ)是非均勻相位常數(shù)，由上圖可知，電流分布具有對(duì)稱性，則該分布對(duì)應(yīng)的陣列單元輻射陣因子為：

1. X=i=0時(shí)，泰勒方向圖函數(shù) S(x)=1；
2. X=i小于n時(shí)，S(x)為：

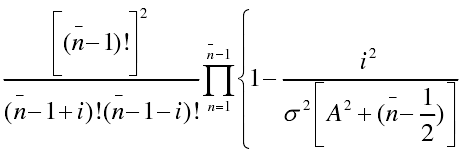
3. X=i大于n時(shí)，S(x)=0。
4. 口徑場(chǎng)分布函數(shù)I(ξ)為：

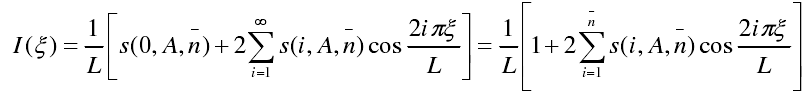
b)離散化

對(duì)于線陣而言，需要對(duì)上圖進(jìn)行離散化，每個(gè)抽樣值對(duì)應(yīng)著直線陣列上的單元激勵(lì)，利用抽樣定理，可以增加抽樣點(diǎn)使陣列單元的對(duì)應(yīng)的幅度分布來(lái)貼合泰勒分布的連續(xù)線源幅度。

離散化后，每個(gè)陣元的坐標(biāo)位置為：

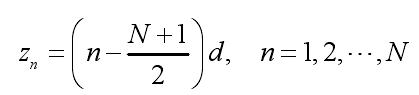
各單元對(duì)應(yīng)的激勵(lì)電流幅度為：

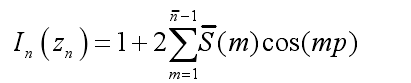
式中，p=2Πz_n/L，L=Nd

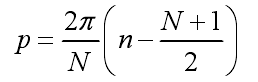
這里的，S(m)為：

1. m=0時(shí)，泰勒方向圖函數(shù) S(m)=1；
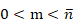2. 時(shí)，S(m)為：

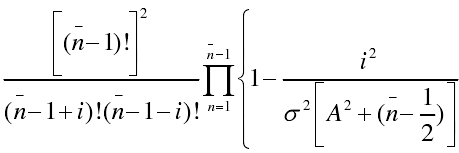
3. 時(shí)，S(m)=0。

該式說(shuō)明，對(duì)泰勒線源進(jìn)行抽樣時(shí)，抽樣結(jié)果只與抽樣點(diǎn)數(shù)相關(guān)，可以看出激勵(lì)幅度與單元數(shù)量有關(guān)，而和單元間距無(wú)關(guān)。

3 聯(lián)合仿真分析

1.陣元數(shù)不變，調(diào)整陣間距

對(duì)于20陣元的天線，分別仿真了間距為λ、λ/2、λ/4情況下的輻射特性，如下圖所示。三種情況下的天線陣元激勵(lì)幅度相同。

單元數(shù)為20，陣元間距d為λ，指向0度

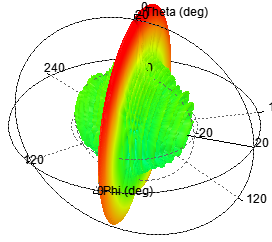
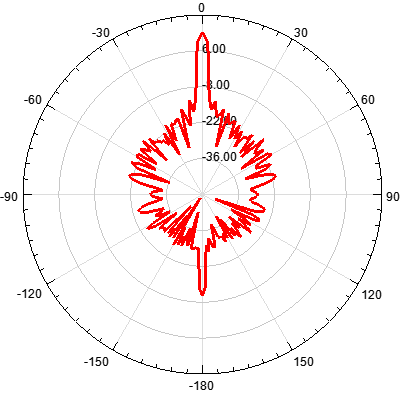
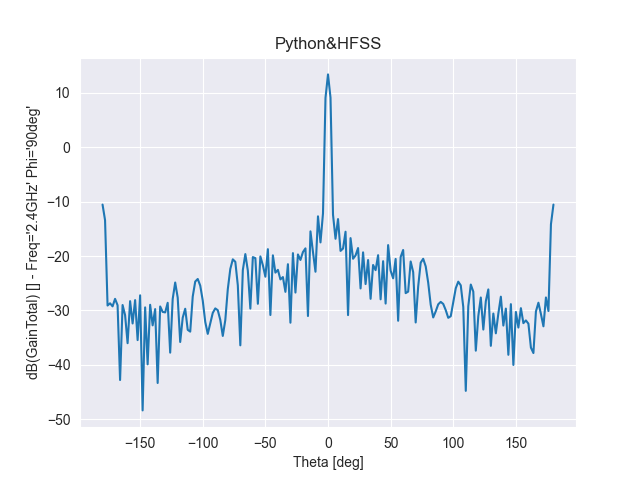
單元數(shù)為20，陣元間距d為λ/2，指向0度

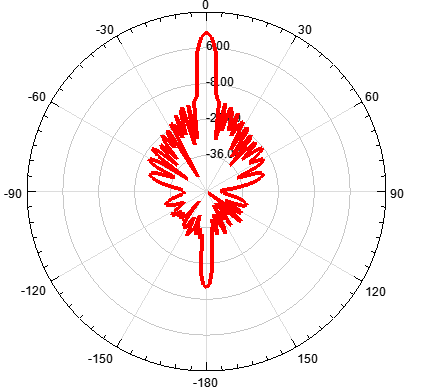
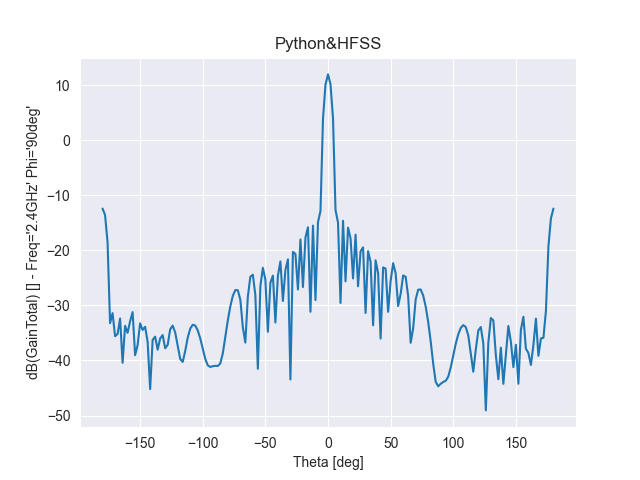
圖 3 d=λ/2輻射特性

單元數(shù)為20，陣元間距d為λ/4，指向0度

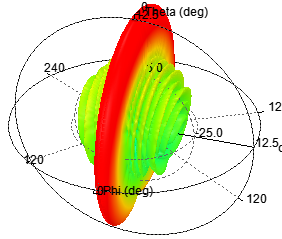
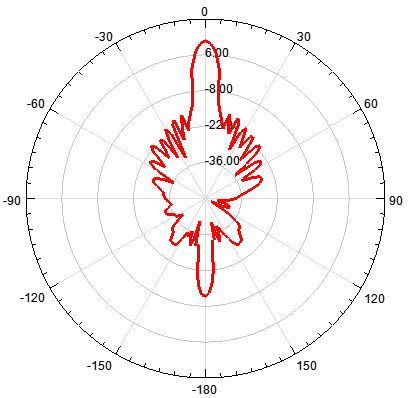
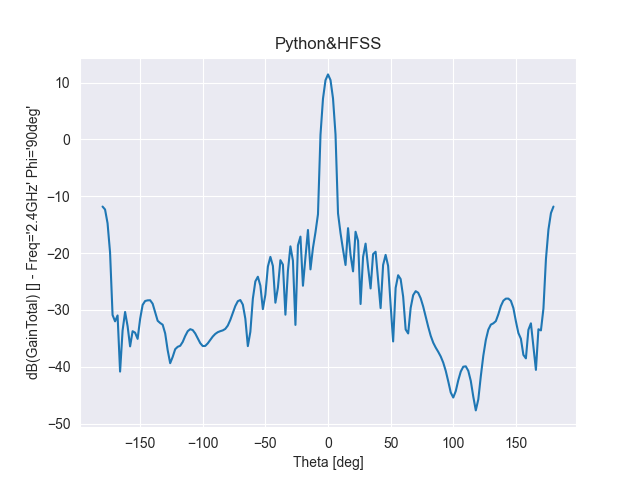
圖 4 d=λ/4輻射特性

2.切比雪夫綜合與泰勒綜合對(duì)比

下面通過(guò)python與HFSS設(shè)計(jì)了兩組12元陣天線，分別采用了切比雪夫綜合法和泰勒綜合法，對(duì)比說(shuō)明兩者的不同之處。

基于切比雪夫綜合法，單元數(shù)為12，陣元間距d為λ/2，指向0度

 

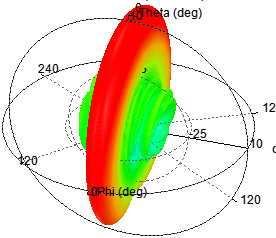
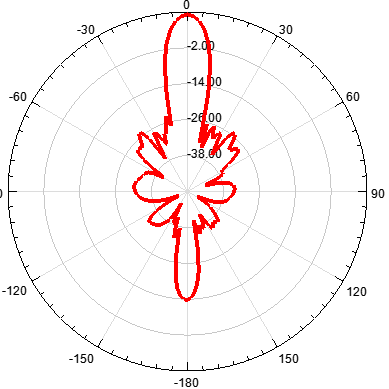
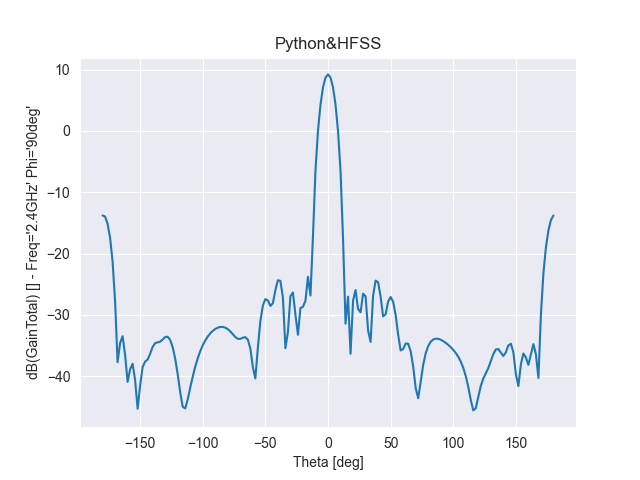
圖 5 切比雪夫綜合法得到的輻射特性

基于泰勒綜合法，單元數(shù)為12，陣元間距d為λ/2，指向0度

 

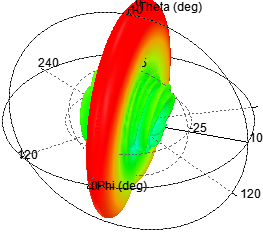
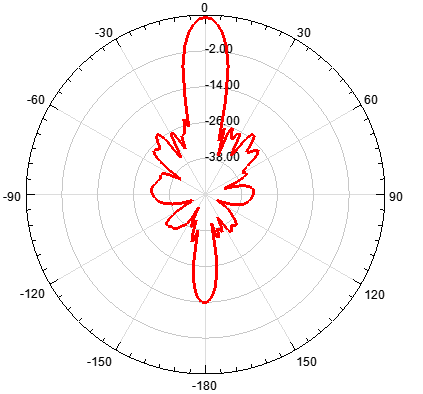
圖 6 泰勒綜合法得到的輻射特性

兩者對(duì)比情況

通過(guò)對(duì)比可知，切比雪夫綜合方法的陣列天線副瓣幅度一致；泰勒綜合法的隨著角度逐漸偏離主瓣，副瓣電平逐次遞減；其次，單元太少則達(dá)不到預(yù)設(shè)值。

4 小結(jié)

由上述分析可知，

1.切比雪夫綜合方法的陣列天線副瓣幅度一致；泰勒綜合法的隨著角度逐漸偏離主瓣，副瓣電平逐次遞減；

2.陣元數(shù)大于13時(shí)，適用泰勒綜合法；

3.單元太少則達(dá)不到預(yù)設(shè)值。

作者：江右射頻